선형대수학개론 1.2
조범희 선생님의 인프런 선형대수학개론 강의를 정리한 내용에, 제가 생각하고 이해한 것을 추가하였습니다.
1.2 Row Reduction and Echelon Forms
A nonzero row or column
At least one element should be nonzero
Nonzero Row 또는 Nonzero Column이 되기 위해서는 최소 하나의 element가 nonzero 여야 한다.
A leading entry of row
A leading entry nof row는 row에서 the leftmost nonzero entry이다.
예를 들어, 아래의 matrix에서
\[\begin{bmatrix} 1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 0 & 0 & 0 & 77\\ 92 & 0 & -1 & 5\\ 0 & 0 & 1 & 0 \end{bmatrix}\]각 row의 leading entry는 다음과 같다.
leading entry or row 1 : 1
leading entry or row 2 : 2
leading entry or row 3 : 77
leading entry or row 4 : 92
leading entry or row 5 : 1
Echelon Form
leading entry를 사용해서 Echelon Form을 정의할 수 있다.
Echelon Form은
- All nonzero rows are above any rows of all zeros.
- Each leading entry of a row is in a column to the right of the leading entry of the row above it
위의 두 조건을 만족해야 한다. 예컨대, 아래 matrix와 같은 꼴을 Echelon Form이라고 한다.
\[\begin{bmatrix} l & * & * & * & * & *\\ 0 & l & * & * & * & *\\ 0 & 0 & l & * & * & *\\ 0 & 0 & 0 & 0 & l & *\\ 0 & 0 & 0 & 0 & 0 & l \end{bmatrix}\]- l stands for leading entry
- * can be any number (zero or non-zero)
여기서, column에서의 조건이 추가되면, Row Reduced Echelon Form을 정의할 수 있다.
Row Reduced Echelon Form
1 & 2. Same with Echelon Form
The leading entry in each nonzero row is 1.
Each leading 1 is the only nonzero entry in its column.
위의 조건을 만족하면 Row Reduced Echelon Form(줄여서 RREF라고 사용)이 되고, 예컨대 아래와 같은 형태를 말한다.
\[\begin{bmatrix} l & * & 0 & 0 & * & 0 & * & 0 & *\\ 0 & 0 & 1 & 0 & * & 0 & * & 0 & *\\ 0 & 0 & 0 & 1 & * & 0 & * & 0 & *\\ 0 & 0 & 0 & 0 & 0 & 1 & * & 0 & *\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & * \end{bmatrix}\]- l stands for leading entry
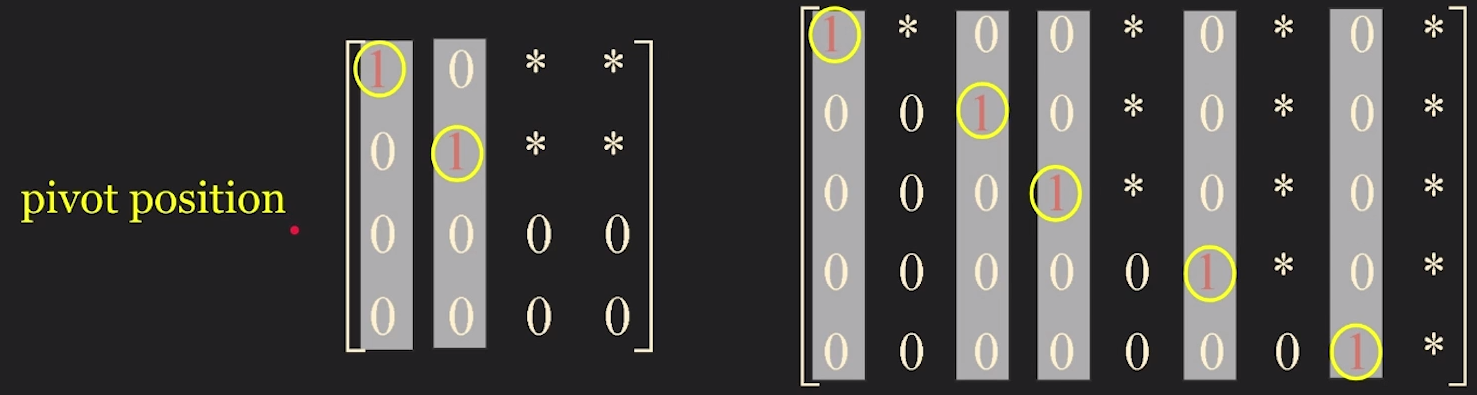
- position of leading entry is called pivot posiotion
그림과 함께 보면, 각 pivot column의 맨 위 position이 pivot position이다.
여기서 RREF에 대한 중요한 정리가 등장한다.
Theorem 1. Uniqueness of the Row Reduced Echelon Form
Each matrix is row equivalent to one and only one reduced echelon matrix.
즉, 어떤 matrix든 단 하나의 Row Reduced Echelon Form을 가진다.
(이는 4단원쯤 가면 증명)
그렇다면, 이러한 RREF를 만드는 Row Reduction Algorithm에 대해 알아보자.
Row reduction algorithm
Row Reduction Algorithm은 임의의 matrix를 Echelon Form을 만드는 Forward Phase와, Echelon Form에서 Row Reduced Echelon Form으로 만드는 Backward Phase로 구성된다.
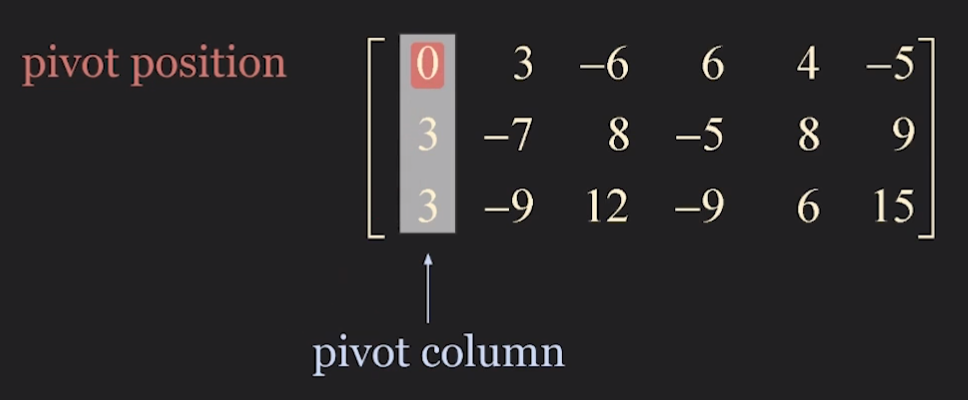
Step1. begin with the leftmost nonzero column
Step 2. select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position
Step3. row replacement to create zeros in all positions below the pivot
~ means row equivalent
Step4. apply stemps 1-3 to the submatrix tha remain
The combination of steps 1-4 is called forward phase
1-4의 과정을 Forward Phase라고 하고, 이 과정이 마친 후의 형태를 Echelon Form이라고 한다.
여기서, Row Reduced Echelon Form을 만들기 위해 이후의 과정을 진행한다.
Step5. Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by a scaling operation.
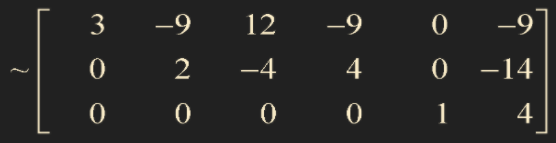 pivot이 1인 해당 column의 나머지 entry를 0으로 만든다
pivot이 1인 해당 column의 나머지 entry를 0으로 만든다
이 Step 5를 backward phase라고 부른다.
그리고 이 때의 형태를 Row Reduced Echelon Form이라고 한다.
Solution of linear systems
이러한 RREF을 사용해서, Linear System의 solution을 판별할 수 있다.
만약, 아래와 같이 어떤 Augmented Matrix의 RREF가 주어졌다고 하자.
\[\begin{bmatrix} 1 & 0 & -5 & 1\\ 0 & 1 & 1 & 4\\ 0 & 0 & 0 & 0 \end{bmatrix}\]이 Matrix는 infinitely many number of solutions를 가진다. 왜냐하면, 이 RREF에서 $x_3$는 Linear System의 다른 변수와 달리 임의로 결정할 수 있기 때문이다. 즉, $x_3$에 따라 무한하게 많은 해가 생긴다. 이때, $x_3$와 같은 variable을 free variable이라고 한다.
Free variable이 아닌 variable을 basic variable 이라고 하는데, 일반적으로 leading position에 해당되는 변수들을 basic variable로 잡고, 나머지는 모두 free variable로 잡는 것으로 약속함으로써 통일성있게 solution을 나타낼 수 있다. 이와 같은 solution 을 general solution 이라고 한다.
여기서, 어떤 Linear System이 갖는 Solution의 Existence와 Uniqueness에 대한 정리를 알아보자
Theorem 2. Existence and Uniqueness Theorem
A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column - that is, if and only if an echelon form of the augmented matrix has no row of the forms $\begin{bmatrix}\ 0\ \cdots\ 0\quad b\ \end{bmatrix}$ with b is nonzero
If a linear system is consistent, then the solution set contains either
i. a unique solution, when there are no free variables
or
ii. infinitely many solutions, when there is at least one free variables.
If a matrix is in row-echelon form, then the first nonzero entry of each row is called a pivot, and the columns in which pivots appear are called pivot columns.




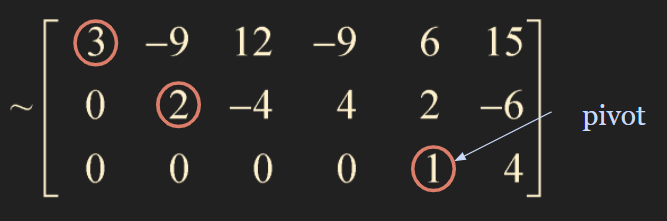


Comments powered by Disqus.